Solid-state sintering
Solid-state sintering is the bonding and densification of particles by the application of heat below the melting point of a material. During sintering, the free surface area of the compact decreases, and this is normally accompanied by an increase in the density, but it is possible for the compact to decrease its surface area and increase its cohesion without a perceptible increase in density. There will be changes in other properties of the compact, such as increased strength, an increase in electrical and thermal conductivity. For most applications, an increase in density is the desired result of sintering. As with any physical process, there must be a lowering of the total internal energy of the system to drive the process. In sintering this reduction in energy is the reduction in the total surface energy of the powder particles due to the replacement of surfaces by grain boundaries and due to coarsening. Overall, the reduction in internal energy is the difference in total surface energy of the powder compact and the remaining surface energy plus the total grain boundary energy of the sintered body.
Although sintering is the oldest method of forming materials from powders, an understanding of the processes occurring during heating of a powder compact is rather recent. Frenkel (1945), who was the first to propose a model for sintering, assumed that sintering occurred by the deformation of crystalline particles under the influence of surface tension, as would occur for amorphous materials such as glass (see Viscous Sintering). However, the predictions of this model did not agree with experimental results using crystalline particles. Kuczynski (1949) demonstrated that sintering occurs by diffusive processes. He proposed several models to describe the early stages of sintering for different transport mechanisms and diffusion paths. Coble (1961) developed models for the later stages of sintering for the case of lattice diffusion or grain boundary diffusion. Although later developments (see reviews by Exner 1979, German 1996, Handwerker et al. 1989, 1990, Rahaman 2008, Kang 2008, Castro et al. 2013 Bordia et al. 2017) have refined these basic ideas, the early models serve well to describe sintering processes. As sintering is a result of diffusive processes, two factors have the major influence on the rate of sintering: temperature (which controls the diffusion rate) and powder particle size (which controls the length scale for diffusion).
Contents
Sintering Stages
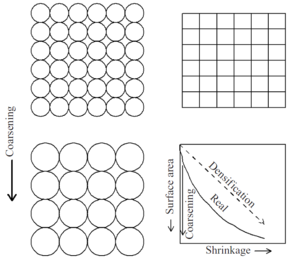
Sintering is conceptually divided into three stages: initial, intermediate, and final, expressing transitions in the connectivity of the particles within an ideal compact of single sized spheres. Within each stage, the pore shape change is well defined and the shrinkage of pores occurs with the pores maintaining a nearly constant shape. The initial stage refers to the growth of contacts or ‘‘necks’’ between the individual powder particles in the compact (Fig. 1). The radius of the necks grown in the initial stage ranges from zero to ~0.2 of the radius of the particles at which point the necks begin to overlap. In the intermediate stage, the pores are approximated as continuous channels coincident with the three-particle junctions (Fig. 2). The final stage begins when the pore channels break up into isolated pores located at the four-grain junctions (Fig. 3). This usually occurs when the density of the sample has increased to ~92% of the theoretical density of the material.
Driving Force for Sintering
During sintering the surface area of the powder compact is reduced. There are two processes that can cause this—coarsening and densification—shown schematically in Fig. 4. For an initial array of n spheres of size R the surface area is n·4πR2. For coarsening of the spheres to a size 2R, the number of spheres must decrease (to conserve mass) by a factor of eight and the surface area will be reduced by a factor of two. Thus, coarsening of the structure results in a reduction of the total surface energy. Notice that in this schematic there is no growth of the contacts between the particles and no decrease in the porosity of the sample. In contrast, if the spherical particles change their shape, the centers of the particles can move together and the volume of the sample will decrease. The surface area is completely converted to grain boundaries with an area of n·2.15R2 (for a cubic array). The energy of a grain boundary is less than the energy of the two free surfaces that are eliminated (typically by about one order of magnitude), and thus the total energy is reduced. A reduction in total energy is a requirement for any process to occur.
The driving force for coarsening and densification arises from the pressure gradients at curved surfaces, and is conceptually described as, ΔP=2γ/R ,where γ is the surface energy and R is the radius of curvature. Although both coarsening and densification result in a reduction in the surface area of the compact, coarsening does not induce densification but lowers the remaining driving force for densification and, as such, is usually an undesired process. Coarsening occurs if surface diffusion is dominating, while densification needs significant rates of grain boundary or volume diffusion. To determine which process dominates, it is necessary to determine the kinetics of these different diffusion mechanisms.
Initial Stage
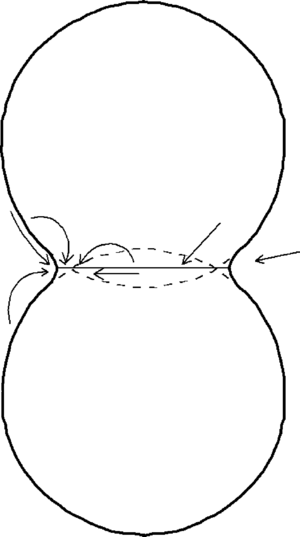
The simplest model for initial stage sintering is the two-sphere model (Fig. 5), that contains all important features necessary for understanding sintering (Exner 1979). The basic premise of the model is that matter is transported from regions of high chemical potential to regions of low chemical potential. In this model, the regions of high chemical potential are at the contact region (grain boundary) and along the convex surface of the sphere. The concave neck region is at a lower chemical potential relative to these areas. Matter can be transported to the neck region through the gas phase (by evaporation from the convex surface and condensation on the concave surface), by surface diffusion (from convex surface to concave surface), lattice diffusion (from either the convex surface or the grain boundary), or grain boundary diffusion. If the source of matter is the grain boundary, the two particle centers approach resulting in densification. If the source of matter is the convex particle surfaces, the two particles change shape without center approach (coarsening). Thus, in the initial stage of sintering, evaporation and condensation and surface diffusion result in coarsening, grain boundary diffusion results in densification and lattice diffusion can result in either, depending on the source of the matter transported.
The driving force for transport during sintering is the difference in chemical concentration between the source of matter (particle surface or grain boundary) and the sink for matter (neck region). The concentrations are different due to the chemical potential differences that result from the curvature differences (Johnson 1978). Along the particle surface the curvature changes from positive at the particle surface to negative at the neck region. Regions of positive curvature correspond to compressive stresses and will have a higher vapor pressure than a flat surface. Conversely, regions of negative curvature will have a tensile stress and a lower vapor pressure than a flat surface. The vapor pressure difference tends to transport matter through the vapor phase into the neck region. The stress difference leads to transport by diffusion to the neck region. Both mechanisms will be active and the total neck growth will be the sum of the two processes. The tensile stress at the neck region is balanced by a compressive stress on the grain boundary. This compressive stress raises the concentration of atoms in the grain boundary region and the tensile stress lowers the concentration of atoms in the neck region. This concentration gradient leads to transport of matter from the grain boundary region to the neck region by grain boundary and lattice transport. In this case, there is densification of the compact.
Many different models have been proposed to describe the initial stage of sintering. In general, each model first assumes a geometry, determines the resulting chemical potential difference that is driving transport, calculates the mass flux based on the geometry and the concentration differences, and then relates the flux to the neck growth rate or the densification rate. If it is assumed that all the transport processes are independent and additive, the rate of neck growth in the initial state can be expressed as:
∂x/∂t=(C_1 γD_l R)/x^2 +(C_2 γD_b R^2)/x^5 +(C_3 γD_s R^2)/x^5 +(C_4 γp_0 R)/x
where x is the radius of the neck, γ is the surface energy, R is the particle radius, Ci is a constant which takes into account the specific diffusion path and the geometry of the model, po is the vapor pressure, and Di is the diffusion coefficient for lattice (l), grain boundary(b), or surface(s) diffusion (Johnson 1978).
Intermediate Stage
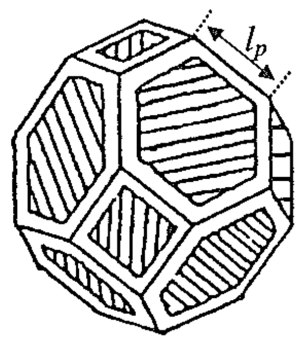
As neck growth proceeds there will be a transition in the pore structure to a system of tubular pores lying along the particle junctions; this is the intermediate stage. In this stage, the pore channels shrink in diameter until the geometry becomes unstable to fluctuations of the surface (Rayleigh instability). While the pore channels can shrink by surface diffusion, the path length for transport becomes very large and, thus, shrinkage is controlled by lattice or grain boundary diffusion (Rahaman 2008). The geometry of the intermediate stage can be envisioned as a truncated octahedron (tetrakaidechedron) simple model of tubular pores intersected by 3 grain boundaries, Fig. 6a. With transport from the grain boundary to the pores, Fig. 6b, the densification rate for lattice diffusion control is 1/ρ (dp/dt)=(10D_l γ_sv Ω)/(ρG^3 kT) When boundary diffusion is the rate controlling mechanism, the densification rate is
1/ρ (dρ/dt)=4/3 [(D_gb δ_gb γ_sv Ω)/(ρ(1-ρ)^(1/2) G^4 kT)]
Modifications to this model have be developed to account for a realistic pore-boundary intersection that includes the dihedral angle. The size dependence, G3 or G4, is not changed but additional terms are included to account for the more complicated geometry of the pore surface.
Final Stage
When the tubular pores have shrunk to the point where they are unstable, they will break up into isolated pores located at the grain junctions. This is the final stage of sintering and is the critical stage for most applications. It is during this stage that the properties of the compact reach the desired values. In the final stage, several factors must be considered in order to understand the process by which pores are eliminated. The driving force for shrinkage of the pores is the difference in concentration between the atoms on the curved surfaces of the pores and the grain boundaries. As the pores are isolated, surface diffusion can only change the shape of the pores. Shrinkage of the pores is controlled by grain boundary and lattice diffusion. For nearly spherical pores the flux of matter, J, to the pore is approximately: J=K_i D_i Δc(rR/(R-r)) where K is a geometric constant, Di is either the lattice or grain boundary diffusion coefficient, ∆c is the concentration difference, r is the radius of the pore, and ℜ is the effective source radius of matter being transported to the pore, roughly half the average distance to the neighboring pores.
Dihedral Angle Effect
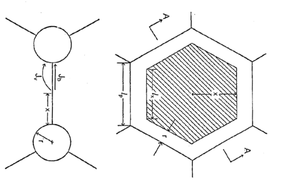
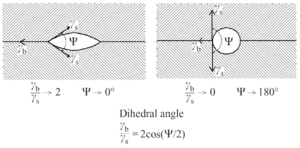
In the discussion of the initial and intermediate stages it was assumed that the dihedral angle of the grain boundary with the pore surface is 180°, implying that the energy of the grain boundary is very much lower than the energy of the surface. As shown in Fig. 3, many pores have dihedral angles of less than 180°. For a pore on a grain boundary, the dihedral angle, ψ, is defined by the ratio of the grain boundary energy, γb, to the surface energy, γs, such that
γ_b/γ_s =2 cos(Ψ/2)
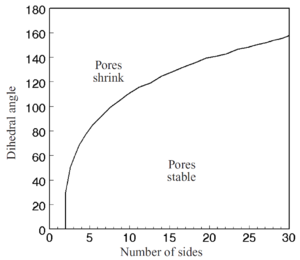
Fig. 7 shows the shapes of pores for different values of the dihedral angle. The curvature of the pore surface increases as the dihedral angle increases, so the driving force for pore shrinkage also increases as the dihedral angle increases. When a pore is located on the junction of three or more grains, the curvature of the pore surface is determined by both the dihedral angle and the number of grains the pore contacts. For a three-sided pore and if ψ = 60° the pore will have straight sides and there will not be a driving force for shrinkage. Hence, this angle is a critical dihedral angle, ψcrit, for pore shrinkage. For a four-sided pore, ψcrit =70.5°. The critical dihedral angle as a function of the number of surrounding grains is shown in Fig. 8 (Kingery and Francois 1967). Thus, when the dihedral angle is too low, pores will be stable in the structure and there will be a limiting density even though removal of the pores would lower the energy of the system. Ultimately, as grain growth occurs the number of grains intersecting the pore will decrease so that pores will become unstable and shrink. However, as the grain size increases, the diffusion distances increase and the shrinkage rate slows down, making pore removal a relatively slow process.
Pore Entrapment
The rate of pore shrinkage given above assumes that the pore is located on a grain boundary. During grain growth, pores can become entrapped inside a grain. In this case, lattice diffusion is the dominant transport mechanism for pore shrinkage and the diffusion distance is the pore–boundary separation distance. Practically, such pores cannot be eliminated during sintering. Pores can become trapped inside a grain if grain growth occurs during final stage sintering. In the intermediate stage of sintering, large pore channels inhibit grain growth due to the strong drag effect of pores on grain boundary motion. As the densification continues and the final stage of sintering is reached, the pores shrink and their drag effect on grain boundary motion decreases until eventually grain boundaries detach from the pores and grain growth occurs and pores become entrapped in the grains. For isolated pores (final stage of sintering) on grain boundaries that contain a gas phase that is insoluble in the lattice, shrinkage will be limited by the rate at which the gas can diffuse to the surface of the sample. This can also lead to a limiting density, but changing the atmosphere during sintering can minimize the effect.
Effects of the heating rate
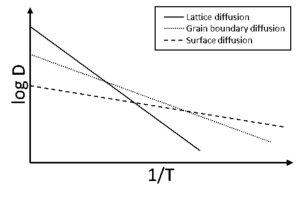
The mass transfer mechanisms during sintering have different temperature dependences due to different thermal activation (Fig. 9). Usually, surface diffusion dominates the sintering process at low temperatures, grain boundary diffusion at intermediate temperatures and volume diffusion at high temperatures. For some materials, some of these processes play no significant role, and some might have additional mass transfer processes as e.g. evaporation and condensation at very high temperatures. As surface diffusion does not result in densification but in coarsening and lowers the driving force for densification, fast heating rates are beneficial for densification as less time is available for surface diffusion coarsening. This rationale resulted in the emergence of the fast firing technique: powder compacts are inserted in a furnace that is pre-heated to the sintering temperature to achieve the fastest possible heating rates. Other techniques that utilize fast heating rates to improve densification are SPS and flash sintering (see below) and laser flash sintering.
Effects of mechanical Pressure
If a mechanical pressure Pa is applied to the system by external means, this pressure adds to the driving force for sintering. However, as the powder compact is not fully dense, the pressure acts on the particle contact area resulting in a higher pressure in the sintering neck area. The effective pressure ΔPeff is higher by a stress intensification factor ϕ:
ΔP_e=ϕP_a The stress intensification factor accounts for the size of the sintering neck relative to the particle size. Usually, it is assumed that ϕ is inversely proportional to the relative density ρ. The modified driving force for sintering is the sum of the two pressures, ΔP=2γ/R+ϕP_a Using this modified driving force for sintering, the shrinkage rate can be obtained for the different diffusion mechanisms and sintering stages as shown in table 1. Note that for P_a=0 the equations reduce to the pressureless densification rates.
Table 1 Densification rate 1/ρ dρ/dt for pressure assisted sintering with different mass transport mechanisms. D is the respective diffusion coefficient (l: lattice, gb: grain boundary), Ω the molecular volume, G the grain size, k the Boltzman constant, γsv the surface energy, r the pore radius. Mechanism Intermediate stage Final stage Lattice diffusion 1/ρ dρ/dt=40/3 ((D_l Ω)/(G^2 kT))(P_a ϕ+γ_sv/r) 1/ρ dρ/dt=40/3 ((D_l Ω)/(G^2 kT))(P_a ϕ+〖2γ〗_sv/r) Grain boundary diffusion 1/ρ dρ/dt=95/2 ((D_gb δ_gb Ω)/(G^3 kT))(P_a ϕ+γ_sv/r) 1/ρ dρ/dt=15/2 ((D_gb δ_gb Ω)/(G^3 kT))(P_a ϕ+〖2γ〗_sv/r) Dislocation motiona 1/ρ dρ/dt=A(Dμb/kT) ((P_a ϕ)/μ)^n 1/ρ dρ/dt=B(Dμb/kT) ((P_a ϕ)/μ)^n a A and B are numerical constants; n is and exponent that depends on the mechanism of dislocation motion.
In general, applying a mechanical pressure is useful for materials where high densities are not achieved with pressure-less sintering as e.g. classically the case for refractory or transparent materials. There are different ways of applying mechanical pressure to a powder compact. Uniaxial pressures are applied in hot pressing and spark plasma sintering (SPS). In hot pressing, a punch-die combination (typically graphite) is used in a vacuum furnace and with a load frame. Heating rates are limited by the furnace (typically <50K/min). Maximum pressures and temperatures are limited by the heater and die materials and are in the order of 2200°C and 100MPa. Spark plasma sintering (SPS) is similar to hot pressing in that a uniaxial pressure is applied to a graphite-based punch-die combination. However, the punch-die combination is heated directly by an electrical current resulting from a voltage between the two rams of the press. While maximum pressures and temperatures are comparable to hot pressing, much higher heating rates (more than 200K/min) can be used, resulting in less time for coarsening during heating as discussed above. SPS sintering is used for refractory materials, but also for applications where a fine-grained microstructure is needed. Hot isostatic pressing (HIP) uses gas pressure in an autoclave. Mostly, nitrogen or argon is used along with graphite heaters. Typical maximum temperatures and pressures are 2200°C and 400MPa. Note that this method only densifies the closed porosity as, for open porosity, the pressure does not load the particle contact area. This requires a pre-sintering to about 94% relative density by conventional sintering. Applying a mechanical pressure to closed porosity can result in a build-up of high gas pressure in the remaining porosity as it shrinks. This pressure can result in pore swelling and de-sintering if high temperatures are subsequently applied without pressure e.g. during pressureless cooling after sintering or during a high-temperature application.
Effects of electric fields and currents
The impact of electric fields and currents on sintering have been observed to greatly affect the densification rate as observed recently in flash sintering. For flash sintering, the powder compact is contacted by electrodes and a voltage is applied during the heating ramp. If the conductivity of the powder compact increases with increasing temperature, an increasing current flow occurs resulting in a direct heating of the sample, until a thermal runaway event occurs. The electric current during flash sintering results in Joule heating of the powder compact and this can result in very high heating rates, many hundred K/min that are beneficial for densification. While SPS sintering does not involve a thermal run-away of the sample, electric currents might flow through the powder compact if its conductivity is higher than the surrounding graphite die. The impact of the electric field itself is controversial and still being investigated. While the electric field is not relevant to the curvature driving force for sintering, it can result in electromigration of charged defects and result in a microstructure gradient and a variation of properties along the electric field. Electric fields can result in the nucleation of additional defects (e.g. point defects and dislocations) that may increase transport. Electrolytic decomposition at the electrodes is another effect than can occur due to electric field assisted sintering.
Effects of constraints
Mechanical constraints inhibit the shrinkage of a powder compact during sintering and can result in anisotropic densification and cracking. Such constraints occur when a powder layer is sintered on a dense substrate or if a composite with different densification rates are co-sintered. In general, the constraint results in a lower densification rate: (ρ ̇/ρ)_constraint=(1+ν)/(1-ν)⋅1/3⋅(ρ ̇/ρ)_free with the shrinkage rate (ρ ̇/ρ), the relative density ρ and the viscous Poisson’s ratio ν. Constraints on sintering frequently result in residual porosity, delamination and sintering distortion due to mechanical stresses developed at the constraint.
Summary
This article follows a encyclopedia articles (Ref 1) and is a summary of the basic ideas of solid-state sintering. Many of the features of sintering are well understood. It is clear from the modeling and experiments that particle size is a dominant factor in controlling sintering rates. Other important parameters are the transport mechanisms that dominates sintering in a given case, heating rates and mechanical pressures. Along with an emerging understanding of these parameters, different sintering techniques are being developed, as e.g. SPS sintering which utilizes fast heating rates and a mechanical load to obtain fast densification.
References
Blendell JE and Rheinheimer WR 2020 Reference Module in Materials Science and Materials Engineering, Elsevier, 2020
Coble R L 1961 Sintering crystalline solids. J. Appl. Phys. 32, 789–92 Exner H E 1979 Principles of single phase sintering. In: (ed.) Reviews on Powder Metallurgy and Physical Ceramics. Freund Publishing House, Israel, Vol. 1, pp. 1–4
Frenkel J 1945 Viscous flow of crystalline bodies under the action of surface tension. J. Phys. USSR 9, 385
German R M 1996 Sintering Theory and Practice. Wiley, New York
Handwerker C A, Blendell J E, Coble R L 1989 Sintering of ceramics. In: Uskokovic D P, Palmour H, Spriggs R M (eds.) Science of Sintering. Plenum Press, New York, pp. 3–37
Handwerker C A, Blendell J E, Kaysser W A, 1990 Sintering of Advanced Ceramics. Ceramic Transactions, Vol. 7. American Ceramic Society, Westerville, OH Johnson D L 1978 Fundamentals of the sintering of ceramics. In: Palmour H, Davis R F, Hare T M (eds.) Processing of Crystalline Ceramics. Plenum Press, New York
Kingery W D, Francois B 1967 Sintering of crystalline oxides. In: Kuczynski G C, Hooton N A, Gibson C F (eds.) Sintering and Related Phenomena. Gordon and Breach, New York, p. 471
Kuczynski G C 1949 Self-diffusion in sintering of metal particles. Trans. AMIE 185, 169–78
Rahaman M N 2008 Sintering of Ceramics. CRC Press, New York
Kang S-J L 2005 Sintering. Elsevier, Boston
Bordia, Rajendra K.; Kang, Suk-Joong L. & Olevsky, Eugene A. Current understanding and future research directions at the onset of the next century of sintering science and technology Journal of the American Ceramic Society, 2017, 100, 2314-2352
Castro, Ricardo H. R. & van Benthem, Klaus (ed.) Sintering: mechanisms of convention nanodensification and field assisted processes Springer, 2013